華爾街的秘密武器:期權定價模型,一文看懂財富密碼!
银行的金融市场交易活动中,期权定价模型是至关重要的工具,它们提供了一套严谨的理论框架和计算方法,用以评估期权的合理价格。这些模型帮助交易员和风险管理者做出明智的决策,管理风险,并把握市场机会。 理解这些模型是银行成功参与金融市场交易的关键。 Black-Scholes 模型是期权定价领域中最经典、应用最广泛的模型之一。它为欧式期权提供了一个简洁而强大的定价公式。
模型假设与关键因素
Black-Scholes 模型基于一系列理想化的假设,例如标的资产价格服从对数正态分布,市场是完全有效的(无摩擦,无交易成本),且在期权有效期内,无风险利率保持不变。
该模型的核心公式考虑了以下几个关键因素:
- 标的资产价格 (S): 当前标的资产的市场价格。
- 执行价格 (K): 期权持有者可以购买或出售标的资产的价格。
- 无风险利率 ®: 在期权有效期内,无风险投资的利率。
- 到期时间 (T): 期权到期的时间长度(通常以年为单位)。
- 标的资产价格波动率 (σ): 标的资产价格在一段时间内的波动程度。
通过将这些因素输入 Black-Scholes 公式,可以计算出理论上的期权价格。虽然存在一定的局限性,但Black-Scholes 模型仍然是金融市场中期权定价的重要基准。
Cox-Ross-Rubinstein 二叉树模型提供了一种直观且易于理解的期权定价方法,尤其适用于美式期权等复杂情况。
模型的直观性与优势
该模型的核心思想是通过构建二叉树来模拟标的资产价格在不同时间步长的变动。在每一个时间节点,资产价格都有两种可能的变化方向:上升或下降。通过设定上升和下降的幅度,以及相应的概率,可以构建出一个完整的价格变动路径。
与 Black-Scholes 模型不同,二叉树模型不需要连续时间的假设,因此在处理以下情况时具有优势:
- 美式期权定价: 美式期权允许持有者在到期日之前的任何时间执行期权。二叉树模型可以通过回溯的方式,计算出每个节点上的最优执行策略,从而确定美式期权的合理价格。
- 分红或其他现金流: 当标的资产在期权有效期内产生分红或其他现金流时,二叉树模型可以更容易地进行调整,以反映这些因素对期权价格的影响。
- 多阶段定价: 对于涉及多个阶段或多种资产的复杂期权,二叉树模型可以提供一个灵活的框架,进行逐步定价。
虽然计算量可能比 Black-Scholes 模型更大,但二叉树模型凭借其直观性和适应性,成为期权定价领域的重要工具。 Garman-Kohlhagen 模型专门用于外汇期权的定价,它充分考虑了外汇市场的独特特性,特别是不同货币之间的利率差异。
模型对外汇市场特性的考量
在外汇市场中,交易的是一种货币相对于另一种货币的价值。因此,外汇期权赋予持有者在未来某个时间以约定汇率买入或卖出特定货币对的权利。
Garman-Kohlhagen 模型对 Black-Scholes 模型进行了扩展,将两种货币的利率纳入考虑范围。具体来说,该模型将一种货币视为支付连续红利的资产,红利率等于该货币的无风险利率。
通过考虑两种货币之间的利率差异,Garman-Kohlhagen 模型能够更准确地反映外汇期权的价值。这对于银行在外汇交易中管理风险、制定交易策略至关重要。 Heston 随机波动率模型与传统的期权定价模型不同,它引入了波动率随机性的概念,更贴合实际市场中波动率的动态变化。
模型对市场波动率变化的适应性
传统的 Black-Scholes 模型假设标的资产的波动率在期权有效期内是一个常数。然而,在现实金融市场中,波动率往往会随着市场情绪、新闻事件等因素而发生变化。
Heston 模型通过引入一个随机过程来描述波动率的变化,使得波动率本身也成为一个随机变量。该模型包含以下关键要素:
- 波动率的随机过程: 描述波动率如何随时间变化的数学模型。
- 波动率的均值回复: 波动率倾向于回到其长期平均水平的特性。
- 波动率的波动率: 波动率本身的波动程度。
通过考虑波动率的随机性,Heston 模型能够更准确地反映期权的价格,尤其是在市场波动较大的情况下。这使得 Heston 模型成为金融机构进行风险管理和复杂期权定价的重要工具。 不同的期权定价模型各有特点,适用于不同的市场环境和交易场景。 下表对以上介绍的几种模型进行了简要对比:
期权定价模型对比
| 模型名称 | 主要特点 | 适用场景 |
|---|---|---|
| Black-Scholes 模型 | 理论基础成熟,计算相对简单 | 欧式期权定价,市场条件相对理想 |
| Cox-Ross-Rubinstein 二叉树模型 | 直观易懂,可处理复杂期权 | 美式期权,多阶段定价 |
| Garman-Kohlhagen 模型 | 考虑外汇市场特性,纳入利率差异 | 外汇期权定价 |
| Heston 随机波动率模型 | 考虑波动率的随机性,更符合实际市场波动情况 | 更复杂的市场环境,波动率变化显著的情况 |
不同模型的特点与适用场景
选择合适的期权定价模型需要综合考虑以下因素:
- 期权类型: 欧式期权、美式期权或其他奇异期权。
- 标的资产: 股票、外汇、商品或其他资产。
- 市场环境: 市场波动率、流动性、利率等因素。
- 数据可用性: 模型所需的历史数据和市场数据。
- 计算成本: 模型的计算复杂度和所需的时间。
银行在实际应用中,会根据具体的交易情况和市场环境,选择最合适的定价模型,或者对模型进行适当的调整和改进,以提高定价的准确性和可靠性。 期权定价模型是金融市场交易的重要工具,但每种模型都有其局限性和适用范围。 银行在实际应用中需要谨慎选择,并不断适应市场变化。
实际应用中的考量与未来发展
在使用期权定价模型时,银行需要关注以下几个方面:
- 模型假设的有效性: 检查模型假设是否与实际市场情况相符。
- 数据质量: 确保输入模型的数据准确可靠。
- 模型风险: 认识到模型可能存在的误差和偏差。
- 市场变化: 随着市场环境的变化,及时调整和更新模型。
模型选择与应用注意事项
此外,随着金融市场的不断发展和创新,新的期权定价模型也在不断涌现和完善。 例如,一些模型考虑了跳跃扩散、随机利率等因素,以更准确地反映复杂市场环境下的期权价格。 金融科技的发展也为期权定价带来了新的机遇。 机器学习、人工智能等技术可以用于提高模型的预测能力和效率。
未来,期权定价模型将朝着更加精细化、智能化和个性化的方向发展,为金融市场交易提供更强大的支持。
股票型基金
MORE>-

揭秘中国股市的“缅A”:国家队、规则与散户的博弈
近年来,不少人谈论着“缅A”,却对这个概念知之甚少。实际上,它指的是...
-

黄金期货趋势预测:技术、基本面与市场情绪的综合分析
黄金期货市场波动剧烈,精准预测其走势是众多投资者追求的目标。然而,黄...
-
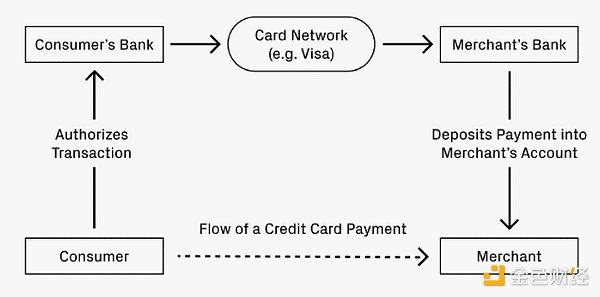
稳定币的未来:借鉴信用卡网络的成功经验
稳定币是近年来最具变革性的支付方式,改变了资金流动的模式,其低廉的跨...
-

ETH 4小时K线图技术分析:短期震荡,谨慎观望
近期ETH价格经历震荡下跌,当前价格在2446.38美元附近运行。4...
-

基金圈大地震!贝莱德、红塔红土同时换帅,背后真相细思极恐!
基金公司高管变动频繁:贝莱德与红塔红土双双换帅近期,基金行业人事...
-
感谢分享石四药集团的公告解读!这篇文章分析得比较全面,结合了资本运作、公司发...
-
感谢分享博时中债5-10农发行A基金的信息!近一年11.23%的收益率看着不...
-
感谢分享ChatGPT的分析,很有参考价值。文中提到的‘拉高出货’和鲸鱼操纵...
-
似水年华 评论文章:金属价格下跌,原因复杂,宏观经济和供需关系是主要因素。区块链技术应用于金属市...
-
跌破10万美元?这波动也太大了!看来特朗普的政策影响比想象中复杂,专家预测更...
- 最近发表
-
- 2025医药基金异军突起:蔡依林、易烊千玺都看好,创新药策略领跑,港股科创板成关键血謎拼圖
- 股市“虚假繁荣”藏隐忧:大盘股护盘难掩空头逆袭,成交量不足需警惕
- 孟耿如关注!美股震荡、孙兴慜赛事:掌握交易真谛,迎接挑战
- 美股震盪避險情緒升,地緣政治推升黃金看漲,國泰金籲配置抗系統風險。
- 金價震盪機遇:懸壺金翁策略、美債殖利率影響與NBA MVP啟示
- 宠物经济万亿商机:源飞宠物营收藏隐忧,蔡力行也关注,威力彩般诱人?
- 有友食品西雅展:鳳爪創新升級,打造國民零食品牌
- 烘焙奧運:中國國際焙烤展揭幕,聖牧塞茵蘇「0芽孢」馬斯卡彭引領清潔標籤革命
- 深交所全球投資者大會:聚焦中國新質生產力,警惕投資風險與挑戰
- 2029加密貨幣:比特幣島興衰、中本聰神話與隱秘圈的覺醒【蘇花公路、fantasy life i】
